Категории:
Полезные Сведенья
Кухонная Философия
Общество и его пороки
Новости
Еда и Питье
Техника
Разное
Личное
Природа
Фото/Видео
"Веселые" Картинки
Юмор
Пишите Письма
Реклама:
| Реклама |
|
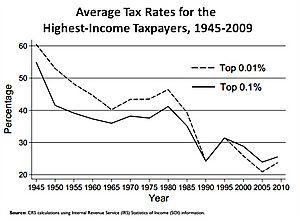
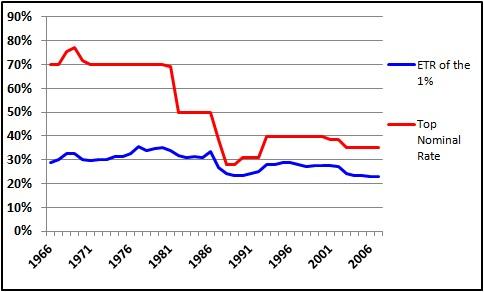
December 2, 2012 Большинству русских читателей, впрочем, это не интересно. Суть в том, что левые в США постоянно утверждают, что налоги за последние 50 лет на "богатых" только снижались и было бы не плохо их повысить. Вот например график из википедии: Тэги: Dec2012 Общество Полезные сведенья Темы, имеющие некоторое отношение к этой (русскоязычный поиск в mysql все же очень не совершенен): А в остальном, прекрасная маркиза, все хорошо, все хорошо January 22, 2012 Таки да, в белый дом завезли особо злые шышки September 28, 2011 AOL по ошибке рассекретила поисковые предпочтения 650 тысяч пользователей August 8, 2006 "Честная доля" November 24, 2014 Вот жеж загадка для социалистов January 15, 2016 Комментировать: Архив:Apr2025 Mar2025 Feb2025 Jan2025 Dec2024 Nov2024 Oct2024 Sep2024 Aug2024 Jul2024 Jun2024 May2024 Apr2024 Mar2024 Feb2024 Jan2024 Dec2023 Nov2023 Oct2023 Sep2023 Aug2023 Jul2023 Jun2023 May2023 Apr2023 Mar2023 Feb2023 Jan2023 Dec2022 Nov2022 Oct2022 Sep2022 Aug2022 Jul2022 Jun2022 May2022 Apr2022 Mar2022 Feb2022 Jan2022 Dec2021 Nov2021 Oct2021 Sep2021 Aug2021 Jul2021 Jun2021 May2021 Apr2021 Mar2021 Feb2021 Jan2021 Dec2020 Nov2020 Oct2020 Sep2020 Aug2020 Jul2020 Jun2020 May2020 Apr2020 Mar2020 Feb2020 Jan2020 Dec2019 Nov2019 Oct2019 Sep2019 Aug2019 Jul2019 Jun2019 May2019 Apr2019 Mar2019 Feb2019 Jan2019 Dec2018 Nov2018 Oct2018 Sep2018 Aug2018 Jul2018 Jun2018 May2018 Apr2018 Mar2018 Feb2018 Jan2018 Dec2017 Nov2017 Oct2017 Sep2017 Aug2017 Jul2017 Jun2017 May2017 Apr2017 Mar2017 Feb2017 Jan2017 Dec2016 Nov2016 Oct2016 Sep2016 Aug2016 Jul2016 Jun2016 May2016 Apr2016 Mar2016 Feb2016 Jan2016 Dec2015 Nov2015 Oct2015 Sep2015 Aug2015 Jul2015 Jun2015 May2015 Apr2015 Mar2015 Feb2015 Jan2015 Dec2014 Nov2014 Oct2014 Sep2014 Aug2014 Jul2014 Jun2014 May2014 Apr2014 Mar2014 Feb2014 Jan2014 Dec2013 Nov2013 Oct2013 Sep2013 Aug2013 Jul2013 Jun2013 May2013 Apr2013 Mar2013 Feb2013 Jan2013 Dec2012 Nov2012 Oct2012 Sep2012 Aug2012 Jul2012 Jun2012 May2012 Apr2012 Mar2012 Feb2012 Jan2012 Dec2011 Nov2011 Oct2011 Sep2011 Aug2011 Jul2011 Jun2011 May2011 Apr2011 Mar2011 Feb2011 Jan2011 Dec2010 Nov2010 Oct2010 Sep2010 Aug2010 Jul2010 Jun2010 May2010 Apr2010 Mar2010 Feb2010 Jan2010 Dec2009 Nov2009 Oct2009 Sep2009 Aug2009 Jul2009 Jun2009 May2009 Apr2009 Mar2009 Feb2009 Jan2009 Dec2008 Nov2008 Oct2008 Sep2008 Aug2008 Jul2008 Jun2008 May2008 Apr2008 Mar2008 Feb2008 Jan2008 Dec2007 Nov2007 Oct2007 Sep2007 Aug2007 Jul2007 Jun2007 May2007 Apr2007 Mar2007 Feb2007 Jan2007 Dec2006 Nov2006 Oct2006 Sep2006 Aug2006 Jul2006 Jun2006 May2006 |